What is power spectral density (PSD), and why is it important?

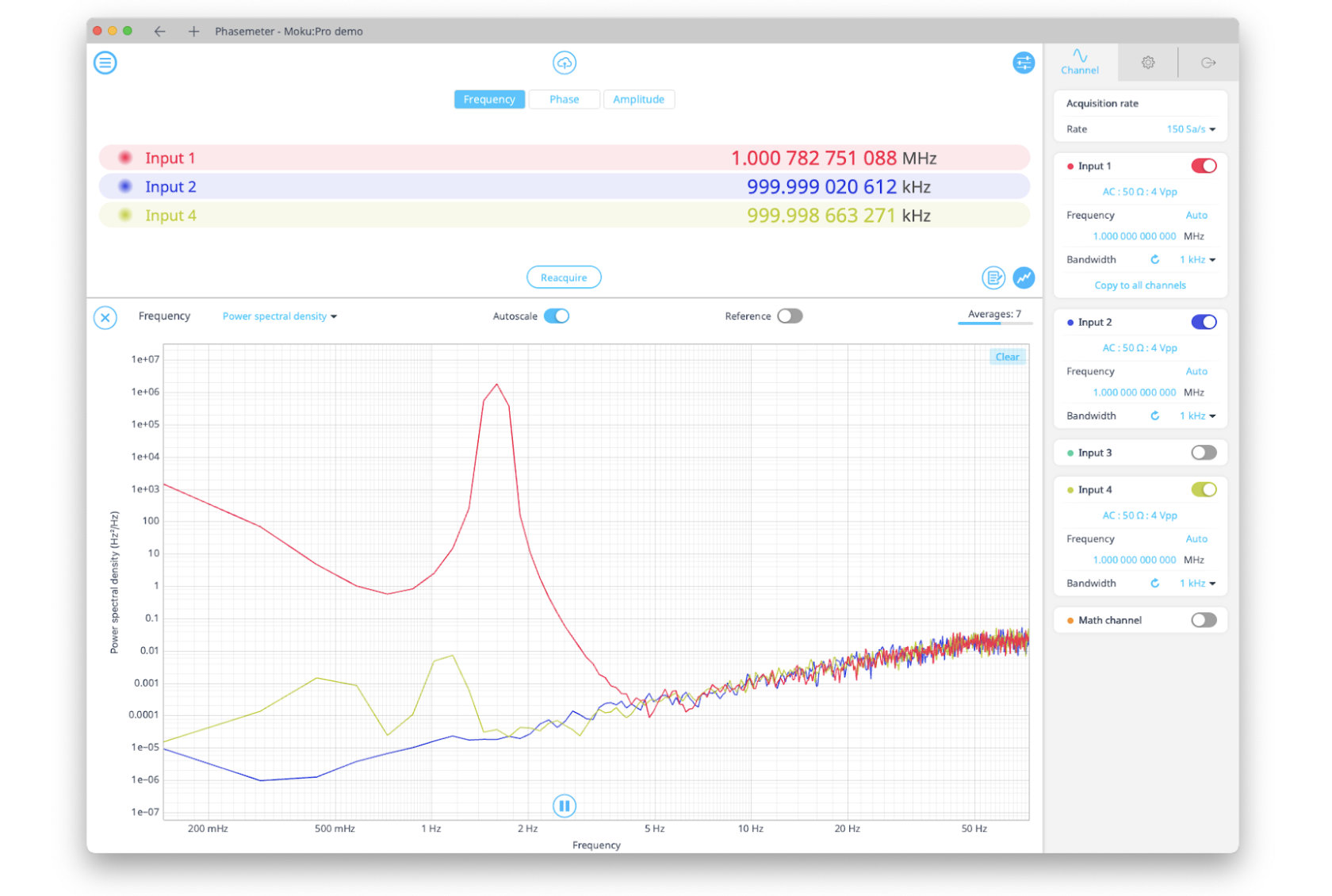
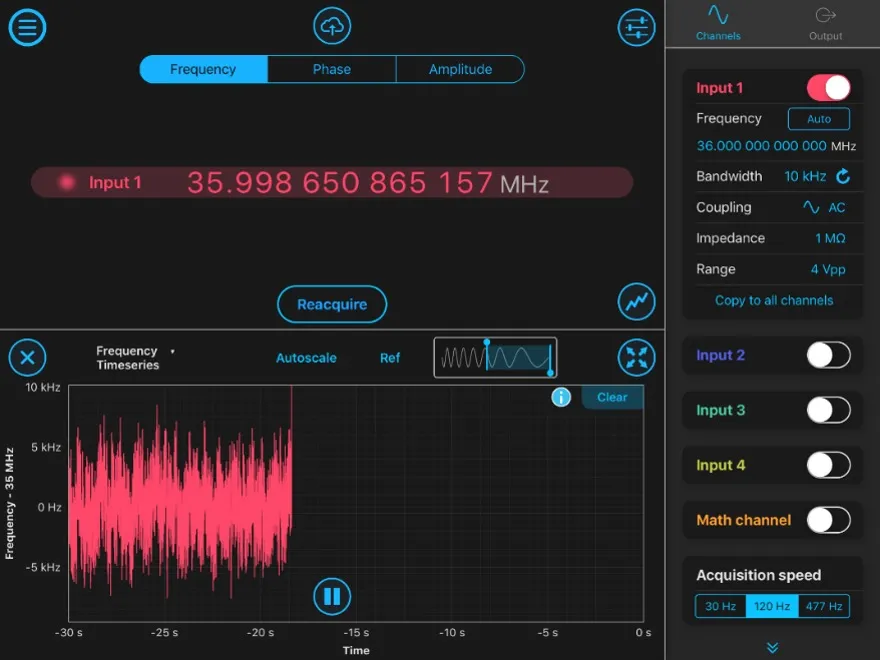
Power spectral density (PSD) is a signal’s distribution of power at different frequencies. While a time-domain analysis watches how a signal changes over time, a frequency-domain analysis like PSD examines how much of the signal’s power is present at different frequencies. For example, Figure 1 shows that Input 1 of the Moku Phasemeter has measured a spike in PSD where the signal’s power is concentrated.

Figure 1: A real-time graph of power spectral density in the Moku Phasemeter.

When is power spectral density used?

Power spectral density allows scientists and engineers to characterize broadband, random signals. This ability is useful in signal processing applications to analyze the frequency content of signals, which helps guide the design of relevant filters. In telecommunications, the PSD enables the analysis of bandwidth usage, noise characterization, and interfering signals. PSD is also useful in radar and sonar applications to track signals and targets of interest.

What is amplitude spectral density?

Amplitude spectral density is the measure of a signal’s amplitude at different frequencies; it’s also the square root of the power spectral density.

How is power spectral density calculated?

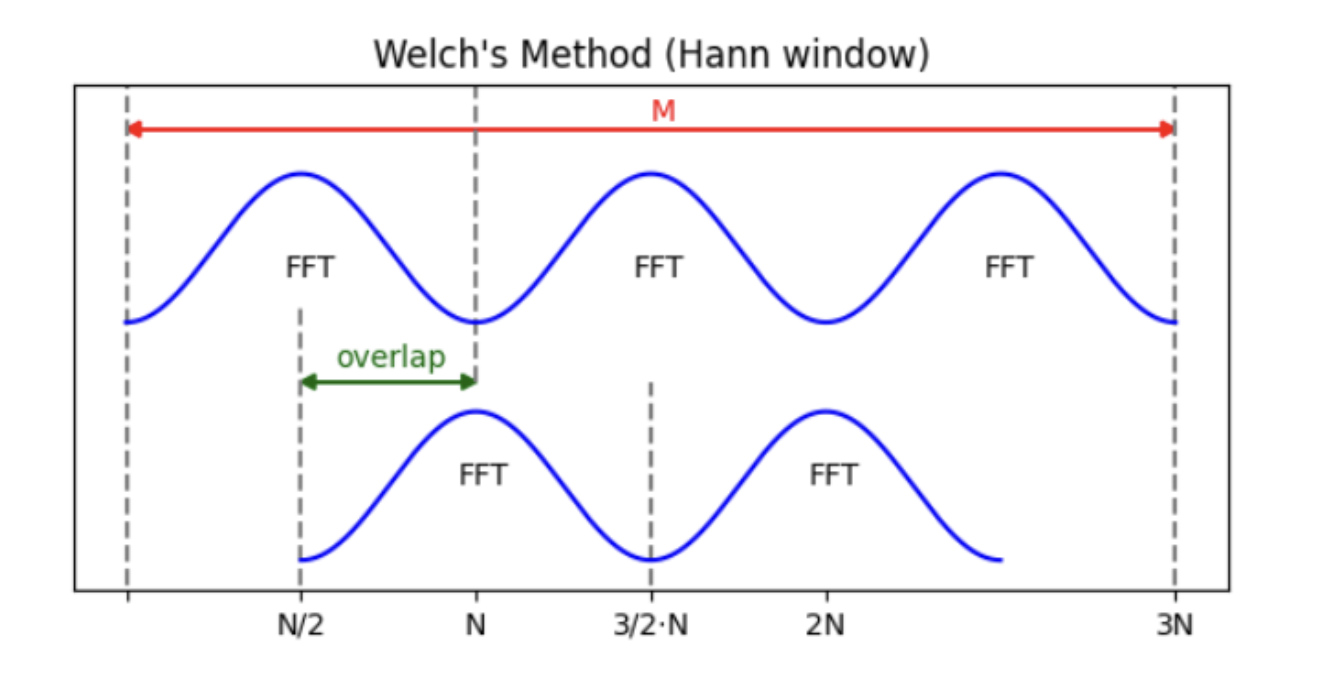
In the Moku Phasemeter, the power spectral density and amplitude spectral density are calculated using Welch’s method of overlapping periodograms, with a 50% overlap and a Hanning window. Depending on the sampling rate selected by the user, the number of points is either 512, 1024, or 2048.

This method, shown in Figure 2, is a popular non-parametric way to calculate power spectral density, using fast Fourier transform (FFT) in the analysis. An FFT allows you to convert a signal from the time domain to the frequency domain. In summary, this method takes modified periodograms of each section and averages them.

Figure 2: An example computation with a 50% overlap in windows, using Welch’s method.

Power spectral density vs. Allan deviation

Power spectral density is the frequency domain counterpart of Allan deviation, shown in Figure 3, which is a common statistical measure to analyze time series data for applications such as oscillator characterization and is the square root of Allan variance. Both values help to describe the stability of a system.

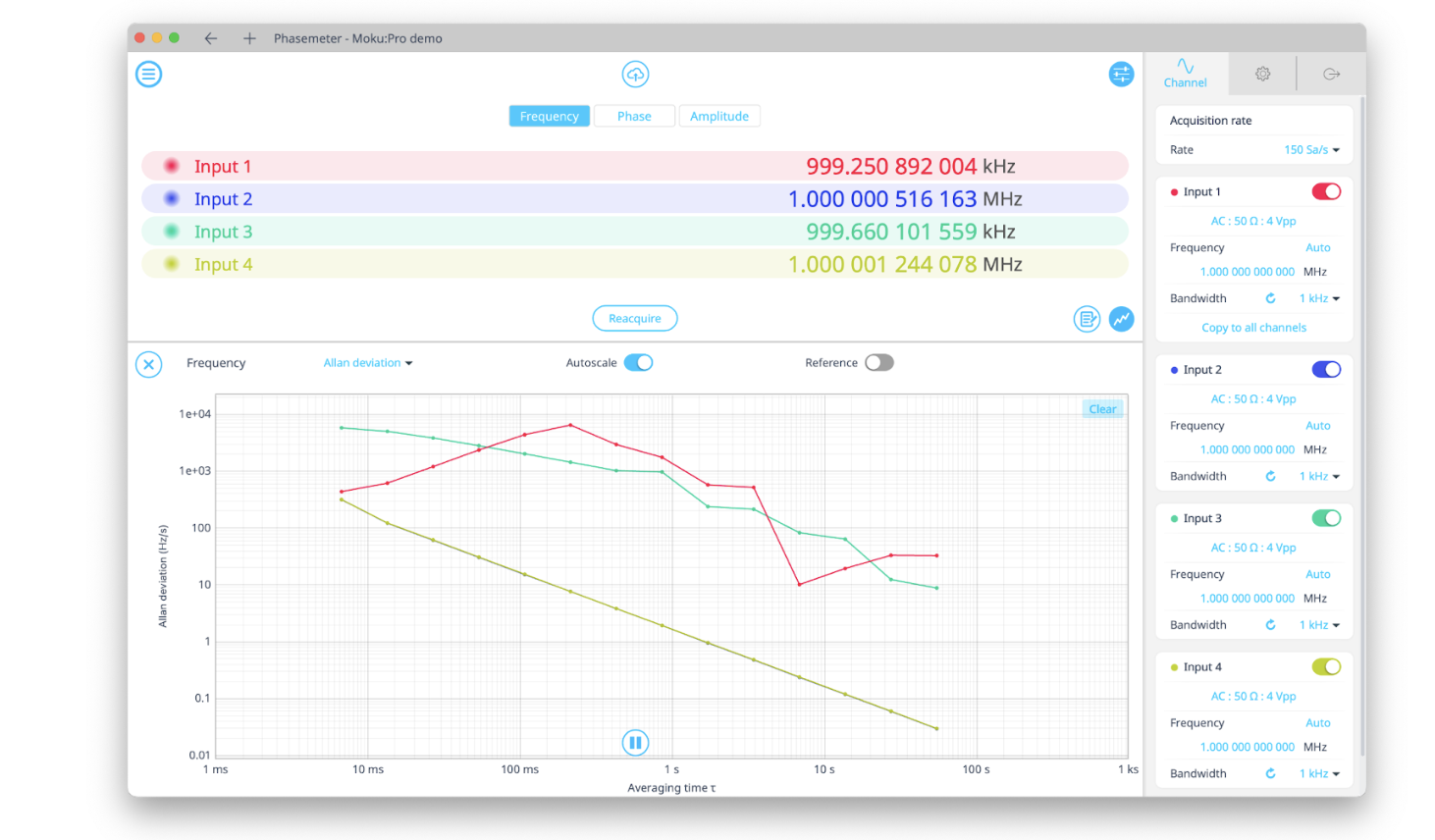
Figure 3: The Moku Phasemeter offers built-in, real-time Allan deviation graphs.

Example: Using power spectral density for dark matter detection

Dark matter detection usually involves an experiment searching for incredibly small signals within a vast sea of noise. These signals, or events, often occur at irregular intervals over long periods of time, making the data collected from these types of experiments very challenging and time-consuming to analyze.

At Los Alamos National Laboratory, researchers used Moku:Pro to collect data, leveraging the flexible Moku Data Logger. Then, using the Moku Python API, they developed a technique to sift through these large data files in search of specific events. To detect low-amplitude events buried in noise, the team first used the Data Logger to track the background noise of the experimental setup. Then, they performed an FFT of this time-series data to determine the PSD.

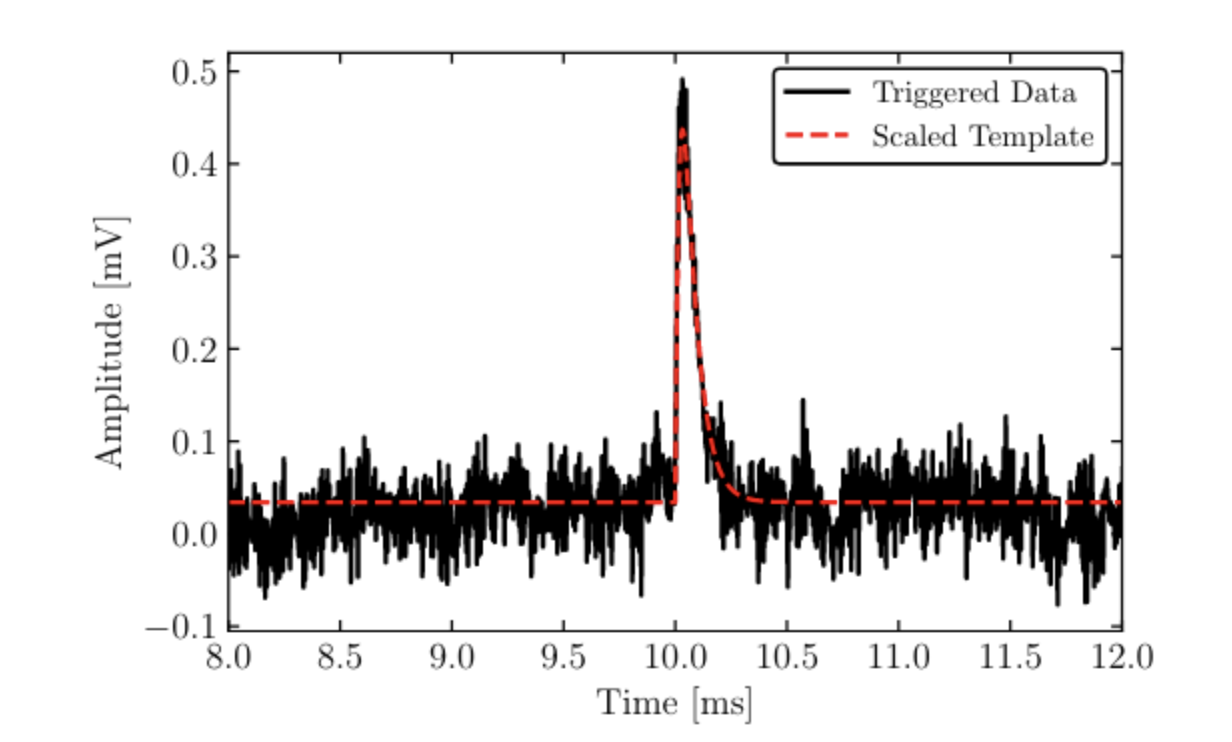
Next, the team supplied their digital acquisition software, called SPLENDAQ, as well as the PSD and an event template, resulting in the data shown in Figure 4. By using a PSD to characterize system noise, the researchers can easily detect extremely low-amplitude events.

Figure 4: Detection of a test event using SPLENDAQ and the Moku Data Logger.

Conclusion

PSD is a crucial tool in signal processing, allowing scientists and engineers to understand the underlying frequency content of signals. While calculating the PSD can be computationally heavy, built-in data visualization tools can reduce post-processing time and allow for better system characterization. Real-time graphs like those in the Moku Phasemeter allow engineers to view their data in parallel with the measurement.

Learn more about the Phasemeter

	Phase detection with the Moku Lock-in Amplifier and Phasemeter The Lock-in Amplifier and Phasemeter are two commonly used instruments to retrieve phase information from oscillating signals. A lock-in amplifier can be considered an open-loop phase detector. The phase is calculated directly from a local oscillator, mixer, and low-pass filter. The Phasemeter implements a digital phase-locked loop (PLL) as its phase detector. A feedback signal is used to update the frequency of the local oscillator. It can be considered a closed-loop approach.
	Modern phase detection: beyond the Lock-in Amplifier In this special presentation, Liquid Instruments Director of Product Ben Nizette shares next-gen strategies for phase detection, and compares traditional lock-in methods with the new wave of dedicated phasemeters.
	Measuring phase with precision: a guide to phase measurement methodologies Accurately measuring phase is a critical aspect of many scientific and engineering applications. Whether you are delving into cutting-edge research, developing sophisticated communication systems, or troubleshooting electronic circuits, the ability to measure phase with precision is indispensable.

If you have a question about a device feature or instrument function, check out our extensive Knowledge Base to find the answers you’re looking for. You can also quickly see popular articles and refine your search by product or topic.

Join our User Forum to stay connected

Want to request a new feature? Have a support tip to share? From use case examples to new feature announcements and more, the User Forum is your one-stop shop for product updates, as well as connection to Liquid Instruments and our global user community.